Φαίνεται απίστευτο, αλλά στο πρόβλημα με τις τρεις πόρτες, που είχαμε θέσει, σάς συμφέρει να αλλάξετε την αρχική σας επιλογή, και μάλιστα, στην περίπτωση αυτή οι πιθανότητες να κερδίσετε διπλασιάζονται. Πριν αρχίσετε να μουρμουρίζετε πάλι ότι δεν ξέρουμε τι μας γίνεται, ρίξτε μια ματιά εδώ: https://en.wikipedia.org/wiki/Monty_Hall_problem.

Το πρόβλημα Monty Hall, όπως ονομάζεται, είναι παλιό, με πληθώρα σελίδων του Διαδικτύου αφιερωμένες σε αναλύσεις του. Αν δε βρήκατε τη σωστή απάντηση, μην ανησυχείτε για την ευφυΐα σας: η συντριπτική πλειοψηφία όσων ερωτώνται απαντούν ότι δεν υπάρχει διαφορά, όποια πόρτα κι αν επιλέξει ο παίκτης. Ολόκληροι πανεπιστημιακοί καθηγητές μαθηματικών έδωσαν λανθασμένες απαντήσεις, και κάποιοι μάλιστα έφτασαν να εκφράσουν τη λύπη τους για την «ελλιπή μαθηματική παιδεία» όσων διαφωνούσαν. Όταν, βέβαια, τους επιδείχθηκε η μαθηματική απόδειξη, ανακάλεσαν.

Το ενδιαφέρον εδώ δεν έγκειται τόσο στην ίδια την απόδειξη όσο στο γεγονός ότι η αντίληψη μας αδυνατεί να παρακολουθήσει την Πραγματικότητα σε ένα απλό, πρακτικό πρόβλημα. Για την αντίληψη των περισσότερων ανθρώπων, όταν πλέον ο παίκτης βρίσκεται αντιμέτωπος με δύο πόρτες, οι πιθανότητες να έχει υποδείξει τη σωστή είναι 50%, ασχέτως επιλογής. Κι όμως...

Υπάρχει πίσω από όλα αυτά μία ευρύτερη συζήτηση, που ξεκινάει από μικρά, καθημερινά πράγματα, όπως το προηγούμενο πρόβλημα, και προχωράει πολύ πιο πέρα, σε θέματα που άπτονται της σύνδεσης μας με τον κόσμο. Κοινή διαπίστωση, απ' όπου κι αν ξεκινήσει κανείς, είναι ότι δεν είμαστε τόσο στέρεα προσδεδεμένοι στην Πραγματικότητα όσο θέλουμε να πιστεύουμε – ότι δεν έχουμε κάποια προνομιακή σχέση μαζί της, ούτε ως άτομα ούτε ως είδος. Προβλήματα όπως το Monty Hall φανερώνουν αδυναμίες μας στην κατανόηση απλών καταστάσεων, και το πράγμα θα τελείωνε εκεί αν οι αδυναμίες αυτές εξαντλούνταν σε ζητήματα διαισθητικής σκέψης και γρίφους αντίληψης. Όμως, η ικανότητα μας να προσλαμβάνουμε την Πραγματικότητα υπολείπεται και σε ένα πολύ πιο θεμελιώδες επίπεδο, που θέτει εν αμφιβόλω, όχι απλώς τις αντιληπτικές μας λειτουργίες, αλλά την επάρκεια της ίδιας της λογικής. Αρκεί να κοιτάξει κανείς στις λεγόμενες θετικές επιστήμες μας για να διαπιστώσει την ύπαρξη ορίων, πέρα από τα οποία δεν μπορούμε να κοιτάξουμε. Χαρακτηριστικά, ο Einstein είχε πει: «Όταν τα μαθηματικά αναφέρονται στην Πραγματικότητα, δεν είναι βέβαια. Όταν είναι βέβαια, δεν αναφέρονται στην Πραγματικότητα». Και εντάξει, θα μπορούσε κανείς να υποστηρίξει ότι τα μαθηματικά είναι από τη φύση τους αφηρημένα· η Φυσική, ωστόσο, δεν αφήνει περιθώρια αμφιβολίας για το πόσο ασύλληπτη και αινιγματική παραμένει η φύση της Πραγματικότητας, ακόμη κι όταν επιχειρούμε να τη στριμώξουμε με έξυπνα πειράματα–παγίδες.

Το ακόλουθο απόσπασμα προέρχεται από το βιβλίο "QeD (Κβαντική Ηλεκτροδυναμική)" του πασίγνωστου φυσικού Richard P. Feynman (ο τονισμός φράσεων είναι δικός μας). Το 1965, ο άνθρωπος αυτός, θρύλος του χώρου του, που κατάφερε μέχρι τέλους να διατηρήσει το αντισυμβατικό του στυλ και το απολαυστικό–επιθετικό του χιούμορ (περιέγραψε το νετρίνο ως «ένα σχεδόν αλλά όχι εντελώς άχρηστο σωματίδιο, όπως λέμε ο γαμπρός σας») τιμήθηκε με το βραβείο Nobel Φυσικής για τη διατύπωση της Κβαντικής Ηλεκτροδυναμικής.

Πριν περάσω στο κύριο θέμα αυτής της διάλεξης, θα ήθελα να σας δείξω με ένα ακόμα πείραμα τον τρόπο που συμπεριφέρεται το φως. Θα σας μιλήσω για την περίπτωση που ένα πολύ ασθενές μονοχρωματικό φως (π.χ. ένα φωτόνιο κάθε στιγμή) φτάνει από μια πηγή S στον ανιχνευτή D (βλ. εικ.49). Ανάμεσα στην πηγή και στον ανιχνευτή τοποθετούμε ένα πέτασμα και ανοίγουμε σ' αυτό δύο πολύ μικρές τρύπες στα σημεία Α και Β, τα οποία απέχουν μεταξύ τους λίγα χιλιοστά του μέτρου. (Αν η απόσταση πηγής – ανιχνευτή είναι 1 μέτρο, οι τρύπες θα πρέπει να έχουν διάμετρο μικρότερη από 0,1 χιλιοστό του μέτρου). Ας υποθέσουμε ότι η πηγή S, η τρύπα Α και ο ανιχνευτής D βρίσκονται στην ίδια ευθεία. έτσι, η τρύπα Β θα βρίσκεται έξω από την ευθεία SAD.

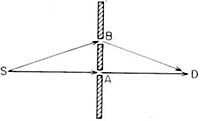
ΕΙΚΟΝΑ 49. Κάθε μία από δύο πολύ μικρές τρύπες (στα Α και Β) ενός πετάσματος, που βρίσκεται ανάμεσα στην πηγή S και στον ανιχνευτή D, αφήνει να περάσει σχεδόν η ίδια ποσότητα φωτός (στην περίπτωσή μας 1%), όταν είναι ανοικτή η μια ή η άλλη. Στη περίπτωση που είναι ανοικτές και οι δύο τρύπες δημιουργείται συμβολή : ο ανιχνευτής δίνει ηχητικά σήματα σε ποσοστό από μηδέν μέχρι 4%. Το ποσοστό εξαρτάται από την απόσταση ανάμεσα στις τρύπες Α και Β (βλ. εικ. 51α).

Αν κλείσουμε την τρύπα Β, ο ανιχνευτής D δίνει ένα ορισμένο αριθμό ηχητικών σημάτων (τακ... τακ... τακ...) που αντιστοιχούν στα φωτόνια που πέρασαν από την τρύπα Α. Έστω ότι για κάθε 100 φωτόνια που φεύγουν από την πηγή S ο ανιχνευτής δίνει 1 τακ· σ' αυτή την περίπτωση μπορούμε να πούμε πως «ο ανιχνευτής λειτουργεί στο l%». Αν κλείσουμε την τρύπα Α και ανοίξουμε την τρύπα Β, θα πάρουμε κατά μέσο όρο από τον ανιχνευτή D –όπως γνωρίζουμε από τη δεύτερη διάλεξη– τον ίδιο αριθμό σημάτων μια και οι τρύπες είναι πολύ μικρές. (Αν «περιορίσουμε» υπερβολικά το φως, οι κανόνες που διαθέτουμε για την συνηθισμένη εικόνα του κόσμου –όπως π.χ. «το φως κινείται σ' ευθεία γραμμή»– καταρρέουν).

Αν όμως αφήσουμε ανοικτές και τις δύο τρύπες, διαπιστώνουμε ένα περίεργο αποτέλεσμα, επειδή εμφανίζεται το φαινόμενο της συμβολής : όταν οι τρύπες βρίσκονται μεταξύ τους σε ορισμένη απόσταση, ο ανιχνευτής δίνει περισσότερα τακ... τακ... τακ... απ' αυτά που περιμένουμε (δηλαδή το 2% = l%+ Ι%) με μέγιστη τιμή που φθάνει στο 4%. Αν οι τρύπες βρεθούν σ' ελάχιστα διαφορετική απόσταση μεταξύ τους, ο ανιχνευτής δεν δίνει κανένα ηχητικό σήμα.

Είναι λογικό να πιστεύετε, ότι ανοίγοντας μια δεύτερη τρύπα στο πέτασμα, θα πρέπει πάντα να φτάνει στον ανιχνευτή μεγαλύτερη ποσότητα φωτός (περισσότερα φωτόνια), κι όμως στην πραγματικότητα αυτό δεν συμβαίνει. Είναι λοιπόν λάθος να λέμε ότι το φως κινείται «είτε με τον ένα είτε με τον άλλο τρόπο». Ακόμα συλλαμβάνω τον εαυτό μου να λέει : «εντάξει, πηγαίνει μ' αυτόν ή με τον άλλο τρόπο», όταν όμως το λέω αυτό, έχω στο μυαλό μου την πρόσθεση των πλατών : το φωτόνιο έχει ένα πλάτος, όταν κινείται με τον ένα τρόπο και ένα πλάτος, όταν κινείται με τον άλλο τρόπο. Αν τα πλάτη είναι αντίθετα, το φως στον ανιχνευτή εξαφανίζεται, παρ' όλο που είναι ανοικτές και οι δύο τρύπες.

Τώρα θα σας μιλήσω γι' άλλη μια παραξενιά της Φύσης. Ας υποθέσουμε ότι τοποθετούμε στις τρύπες Α και Β από έναν ειδικό ανιχνευτή (μπορούμε να επινοήσουμε έναν ανιχνευτή που να διαπιστώνει τη διέλευση ενός φωτονίου από τη τρύπα). έτσι στην περίπτωση που είναι ανοικτές και οι δύο τρύπες, θα μπορούμε να ξέρουμε από ποια τρύπα έχει περάσει ένα φωτόνιο για να φτάσει στον ανιχνευτή D (βλ. εικ. 50). Επειδή η πιθανότητα για να φτάσει ένα συγκεκριμένο φωτόνιο από το S στο D, επηρεάζεται μόνο από την απόσταση ανάμεσα στις δύο τρύπες, θα μπορούσαμε να υποθέσουμε ότι το φωτόνιο με κάποιον «ύπουλο τρόπο» χωρίζεται στα δύο κι ' ύστερα τα δύο κομμάτια ενώνονται πάλι σ' ένα φωτόνιο. Σωστά; Σ' αυτήν την περίπτωση όμως οι ειδικοί ανιχνευτές που βρίσκονται στα Α και Β θα πρέπει να δώσουν ταυτόχρονα «τακ» (μήπως στη μισή ένταση;), ενώ ο ανιχνευτής D θα πρέπει να λειτουργεί με μια πιθανότητα που κυμαίνεται από το μηδέν μέχρι το 4% και η οποία κάθε φορά εξαρτάται από την απόσταση ανάμεσα στα Α και Β.

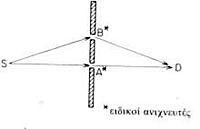
ΕΙΚΟΝΑ 50. Το πείραμα τροποποιείται όταν, στην περίπτωση που είναι ανοικτές και οι δύο τρύπες, τοποθετήσουμε ειδικούς ανιχνευτές ώστε να διαπιστώνουμε μέσω ποιας τρύπας κινείται το φωτόνιο. Επειδή περνά πάντα μέσα από τη μια ή την άλλη τρύπα, θα υπάρχουν δύο διακρίσιμες τελικές καταστάσεις: 1) θα λειτουργούν οι ανιχνευτές στα Α και D και 2) θα λειτουργούν οι ανιχνευτές στα Β και D. Σε κάθε περίπτωση η πιθανότητα να πραγματοποιηθεί το συμβάν είναι 1% περίπου. Οι πιθανότητες των δύο συμβάντων προσθέτονται κανονικά, κι έτσι εξηγείται η πιθανότητα του 2% για τη λειτουργία του ανιχνευτή D (βλ. εικ. 51β).

Να όμως τι συμβαίνει πραγματικά : οι ειδικοί ανιχνευτές στα Α και Β δεν δίνουν ποτέ ηχητικά σήματα μαζί∙ είτε λειτουργεί ο Α είτε ο Β. Το φωτόνιο δεν χωρίζεται στα δύο· κινείται είτε με τον ένα είτε με τον άλλο τρόπο. Επίσης, κάτω απ' αυτές τις συνθήκες (με τους ειδικούς ανιχνευτές), ο ανιχνευτής που βρίσκεται στο D «λειτουργεί στο 2%» (δηλαδή στο απλό άθροισμα των πιθανοτήτων για τα Α και Β : 1 %+ 1 %). Και κάτι ακόμα : το 2% είναι σταθερό και ανεξάρτητο από την απόσταση ανάμεσα στα Α και Β. Με άλλα λόγια, όταν τοποθετούμε τους ειδικούς ανιχνευτές στα Α και Β, κι έτσι γνωρίζουμε από ποια τρύπα περνούν τα φωτόνια, το φαινόμενο της συμβολής εξαφανίζεται!

Η Φύση έχει «μαγειρέψει» με τέτοιο τρόπο τα πράγματα, ώστε να μη μπορούμε ποτέ να αντιληφθούμε το πώς τα καταφέρνει : αν χρησιμοποιήσουμε συσκευές για ν' ανακαλύψουμε με ποιο τρόπο κινήθηκε το φως, τα καταφέρνουμε ωραία και καλά, μόνο που θα έχουμε εξαφανίσει το θαυμάσιο φαινόμενο της συμβολής. Αν όμως δεν χρησιμοποιήσουμε όργανα που να μας λένε με ποιο τρόπο κινήθηκε το φως, τότε ξαναβρίσκουμε το φαινόμενο της συμβολής. Πολύ παράξενο στ' αλήθεια.

Για να καταλάβετε καλύτερα αυτό το παράδοξο, θα σας θυμίσω μια πολύ σημαντική αρχή : για να υπολογίσουμε σωστά την πιθανότητα ενός συμβάντος, θα πρέπει προσεκτικά και επακριβώς να ορίσουμε το πλήρες συμβάν – ειδικότερα τις αρχικές και τις τελικές συνθήκες του πειράματος. Παρατηρούμε προσεκτικά τα όργανα πριν και μετά το πείραμα κι αναζητούμε τις μεταβολές. Όταν υπολογίζαμε την πιθανότητα στη κίνηση ενός φωτονίου από το S στο D χωρίς ανιχνευτές στα Α και Β, το συμβάν περιλάμβανε μόνο τη δημιουργία ενός ηχητικού σήματος από τον ανιχνευτή D. Όταν η μόνη μεταβολή στις συνθήκες είναι το ηχητικό σήμα στον ανιχνευτή D, δεν υπάρχει κανένας τρόπος να πληροφορηθούμε από ποια τρύπα πέρασε το φωτόνιο και έτσι έχουμε το φαινόμενο συμβολής. Το πρόβλημα αλλάζει όταν τοποθετούμε τους ανιχνευτές στις τρύπες Α και Β. Τώρα έχουμε δύο πλήρη συμβάντα, δύο σύνολα τελικών συνθηκών που διακρίνονται μεταξύ τους: 1) λειτουργούν οι ανιχνευτές που βρίσκονται στα Α και D. και 2) λειτουργούν οι ανιχνευτές που είναι στα Β και D. Όταν σ' ένα πείραμα έχουμε πολλές τελικές καταστάσεις, θα πρέπει να υπολογίζουμε την πιθανότητα κάθε μιας απ' αυτές ως ένα ξεχωριστό πλήρες συμβάν.

Για να υπολογίσουμε το πλάτος που αντιστοιχεί στην περίπτωση της λειτουργίας των ανιχνευτών Α και D, «πολλαπλασιάζουμε» τα βέλη που αντιστοιχούν στα ακόλουθα βήματα : α) ένα φωτόνιο από το S πηγαίνει στο Α . β) το φωτόνιο από το Α πηγαίνει στο D και γ) ο ανιχνευτής D δίνει ένα ηχητικό σήμα. Το τετράγωνο του τελικού βέλους είναι η πιθανότητα του συμβάντος, δηλαδή 1 %, η ίδια με την περίπτωση που θα ήταν κλειστή η τρύπα Β (μια και οι δύο περιπτώσεις περιλαμβάνουν τα ίδια βήματα). Το δεύτερο πλήρες συμβάν είναι η λειτουργία των ανιχνευτών Β και D. Η πιθανότητα αυτού του δεύτερου συμβάντος υπολογίζεται με τον ίδιο τρόπο και βρίσκεται να έχει την ίδια τιμή με την προηγούμενη : 1 % περίπου.

Αν τώρα θέλαμε να ξέρουμε πόσο συχνά λειτουργεί ο ανιχνευτής D χωρίς να νοιαζόμαστε αν λειτούργησε ο ανιχνευτής στο Α ή στο Β, η πιθανότητα θα είναι ίση με το άθροισμα των πιθανοτήτων των δύο συμβάντων, δηλαδή 2%. Γενικά, αν στο σύστημα υπάρχει κάτι που το παραλείψαμε και που αν το παρατηρούσαμε, θα μπορούσαμε να πούμε από πού κινήθηκε το φωτόνιο, θα έχουμε διαφορετικές «τελικές καταστάσεις» (διακρίσιμες τελικές συνθήκες) και σ' αυτή την περίπτωση προσθέτουμε τις πιθανότητες για κάθε τελική κατάσταση και όχι τα πλάτη (1).

Έδωσα μεγάλη έμφαση σ' αυτά τα πράγματα, γιατί όσο περισσότερο σας αποκαλύπτεται η παράξενη συμπεριφορά της Φύσης, τόσο δυσκολότερο είναι να δημιουργήσετε ένα μοντέλο που θα εξηγεί τέλεια ακόμα και τα απλούστερα φαινόμενα. Γι' αυτόν ακριβώς το λόγο η Θεωρητική Φυσική παραιτήθηκε απ' αυτή την προσπάθεια.

(1). Η πλήρης ανάπτυξη αυτής της περίπτωσης παρουσιάζει αρκετό ενδιαφέρον : όταν οι ανιχνευτές στα Α και Β δεν είναι τέλειοι και ανιχνεύουν φωτόνια μόνο για κάποιο μέρος του χρόνου, θα έχουμε τρεις διακρίσιμες τελικές καταστάσεις: 1) λειτουργούν οι ανιχνευτές στα Α και D 2) λειτουργούν οι ανιχνευτές στα Β και D και 3) λειτουργεί μόνον ο ανιχνευτής D και όχι οι ανιχνευτές στα Α και Β – δηλ. παραμένουν στην αρχική τους κατάσταση. Οι πιθανότητες για τα δύο πρώτα συμβάντα υπολογίζονται όπως εξηγήσαμε παραπάνω. (με τη διαφορά ότι υπάρχει ένα ακόμα βήμα : μια σμίκρυνση για την πιθανότητα που λειτουργεί ο ανιχνευτής στο Α ή στο Β, επειδή οι ανιχνευτές δεν είναι τέλειοι). Όταν λειτουργεί μόνον ο D αδυνατούμε να διακρίνουμε τις δύο περιπτώσεις και η Φύση παίζει μαζί μας εμφανίζοντας τη συμβολή. Το ίδιο παράξενο αποτέλεσμα θα παίρναμε, αν δεν υπήρχαν οι ανιχνευτές (με τη διαφορά ότι το τελικό βέλος έχει σμικρυνθεί κατά το πλάτος που αντιστοιχεί στους ανιχνευτές που δεν λειτουργούν). Το τελικό αποτέλεσμα είναι ένα μίγμα, δηλαδή το απλό άθροισμα των τριών περιπτώσεων (βλ. εικ. 51). Όσο αυξάνεται η αξιοπιστία των ανιχνευτών, τόσο μικρότερη συμβολή θα παρατηρούμε.

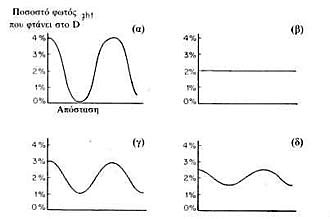
ΕΙΚΟΝΑ 51. Όταν στο Α ή στο Β δεν υπάρχουν ανιχνευτές, συμβαίνει συμβολή – η ποσότητα του φωτός κυμαίνεται από μηδέν μέχρι 4% (α). Όταν στα Α και Β υπάρχουν ανιχνευτές 100% αξιόπιστοι, δεν συμβαίνει συμβολή – η ποσότητα του φωτός που φθάνει στο D είναι σταθερή, 2% (β). Όταν στα Α και Β οι ανιχνευτές δεν είναι 100% αξιόπιστοι, (δηλαδή όταν δεν ανιχνεύονται μερικά φωτόνια απ' αυτά που περνούν από το Α ή το Β), έχουμε τρεις δυνατές τελικές καταστάσεις : να λειτουργούν οι ανιχνευτές Α και D, να λειτουργούν οι ανιχνευτές Β και D, και να λειτουργεί μόνο ο ανιχνευτής D. Έτσι, η τελική καμπύλη που παίρνουμε, προέρχεται από ένα μίγμα συνεισφορών κάθε δυνατής τελικής κατάστασης. Όσο λιγότερο αξιόπιστοι είναι οι ανιχνευτές Α και Β, τόσο μεγαλύτερη θα είναι η συμβολή. Έτσι, στην περίπτωση (γ) οι ανιχνευτές είναι λιγότερο αξιόπιστοι από αυτούς της περίπτωσης (δ). Η συμβολή καθορίζεται από την ακόλουθη αρχή : για κάθε μία από τις διαφορετικές τελικές καταστάσεις η πιθανότητα πρέπει να υπολογίζεται ανεξάρτητα, προσθέτοντας βέλη και υψώνοντας στο τετράγωνο το μήκος του τελικού βέλους· στη συνέχεια προσθέτονται κανονικά αυτές οι μερικές πιθανότητες.

Τα προηγούμενα δεν προέρχονται από κανέναν θεωρητικό αμπελοφιλόσοφο, αλλά από έναν κορυφαίο φυσικό, ο οποίος, μεταξύ άλλων, συμμετείχε στο σχεδιασμό της πρώτης ατομικής βόμβας. Ούτε αφορούν κάποια νεφελώδη θεωρία, αλλά συγκεκριμένο, επαναλήψιμο πείραμα, πασίγνωστο στην επιστημονική κοινότητα. Εκείνο, λοιπόν, που αποκαλύπτεται μέσα από το απόσπασμα είναι ο θεμελιώδης ρόλος του Παρατηρητή. Το ρόλο αυτό στο σχετικό πείραμα παίζουν οι ανιχνευτές φωτός. Συγκεκριμένα, όπως σημειώνει ο Feynman, το φαινόμενο της συμβολής εξαφανίζεται μόλις στη διάταξη προστίθενται ανιχνευτές–παρατηρητές, ενώ, ακόμη πιο αινιγματικά, όταν οι ανιχνευτές–παρατηρητές έχουν μερική μόνο αξιοπιστία, το φαινόμενο της συμβολής διατηρείται σε βαθμό αντιστρόφως ανάλογο της αξιοπιστίας αυτής. Όταν η αξιοπιστία των ανιχνευτών–παρατηρητών είναι μηδενική (π.χ. χαλασμένοι ανιχνευτές), η συμβολή εκδηλώνεται στο ακέραιο. Όταν τοποθετούνται απόλυτα αξιόπιστοι ανιχνευτές–παρατηρητές, η συμβολή εξαφανίζεται. Όταν οι ανιχνευτές–παρατηρητές λειτουργούν σε ποσοστό μικρότερο του 100% της καταγραφικής τους ικανότητας, η συμβολή εκδηλώνεται εν μέρει μόνο!

Θυμηθήκαμε, παρεμπιπτόντως, στο σημείο αυτό κάτι βαρυφορτωμένους με ηλεκτρονικά μηχανήματα ερευνητές που καταφθάνουν σε περιτριγυρισμένους από παράξενες διηγήσεις τόπους, φιλοδοξώντας να αποδείξουν, άλλοι την ύπαρξη και άλλοι τη μη ύπαρξη των όποιων φαινομένων. Δεν καταλαβαίνουν ότι, με τα διάφορα καλώδια να κρέμονται από τις τσέπες και τις κεραίες να εξέχουν από τους γιακάδες τους, είναι σαν να προσπαθούν να συλλάβουν το σκοτάδι φωτίζοντας το με φακό.

Παράλογο; Ασφαλώς. Αυτό ακριβώς υποδεικνύει ο Feynman όταν αναφέρεται στην αδυναμία της Φυσικής, και κατ' επέκταση κάθε ανθρώπινης επιστήμης, να αναλύσει και να μοντελοποιήσει οτιδήποτε πέρα από κάποιο όριο. Αυτό το παρά–λογο, το εξωλογικό, υπάρχει στο κέντρο όλων των κοσμολογιών, θρησκειών και μυθολογιών, όλων των λαών του κόσμου, από την αυγή ακόμα της ανθρωπότητας. Ποιος είπε ότι η ανθρώπινη λογική είναι παντοδύναμη; Ποιος είπε ότι η Πραγματικότητα και τα διάφορα φυσικά –για να μην αναφερθούμε στα παραφυσικά– φαινόμενα δίνουν δεκάρα για την περίφημη, υπερτιμημένη λογική μας και το τι εμείς πιστεύουμε;

Σας ακούγονται εξωφρενικά τα παραπάνω; Αφεθείτε για λίγο να κοιτάξετε τον ουρανό μια ξάστερη νύχτα. Αφεθείτε να αναλογιστείτε τις ανείπωτες εσχατιές του Χώρου, που γεννούν τον τρόμο σε κάθε ανθρώπινο μυαλό. Αφεθείτε να υποψιαστείτε τον απελπιστικά ασύλληπτο αριθμό και τις απίστευτες ιστορίες των κόσμων που υπάρχουν εκεί. Αφεθείτε να ακούσετε το ανυπόφορο ψιθύρισμα του αιώνιου Χρόνου.

Γνωσιολογικά πειράματα έχουν δείξει ότι ο ανθρώπινος νους αδυνατεί να συλλάβει σύνολα με περισσότερα από επτά επιμέρους στοιχεία. Όταν τα μεμονωμένα στοιχεία υπερβαίνουν τον αριθμό αυτό, ο νους μας απλώς προσδίδει στο πλήθος ένα νούμερο, χωρίς ωστόσο να μπορεί να τα συλλάβει ως σύνολο. Έτσι, όταν π.χ. λέμε ότι ένας μήνας έχει τριάντα μέρες, κατανοούμε την τάξη μεγέθους του αριθμού των ημερών, όμως δεν μπορούμε να συλλάβουμε το σύνολο και να απεικονίσουμε στο μυαλό μας τις επιμέρους μέρες ταυτόχρονα. Σκεφτείτε τώρα τα δισεκατομμύρια των άστρων του δικού μας μόνο γαλαξία, και τα δισεκατομμύρια των γαλαξιών του ορατού μόνο Σύμπαντος. Αναλογιστείτε, στην άλλη άκρη του φάσματος, την ατέρμονη διαβάθμιση και την απειρική πολυπλοκότητα του μικρόκοσμου, με τις δομές που κρύβονται εκεί, αόρατες τόσο στα μάτια όσο και στα πιο εκλεπτυσμένα επιστημονικά μας όργανα. Όλα αυτά αποτελούν ένα μέρος μόνο όσων η Πραγματικότητα αφήνει να κρυφοκοιτάξουμε μέσα από τη χαραμάδα των αισθήσεων και της λογικής μας.

Τι είναι, λοιπόν, πιο εξωφρενικό, η απειρία αυτή, ή η ιδέα του ανθρώπου ότι μπορεί να την προσαρμόσει στα μέτρα της λογικής του, σε τοιχώματα από καθολικές κοσμοθεωρίες, απόλυτες γνώσεις και τελικές αλήθειες; Μπορούν όλες μαζί οι θεωρίες μας να χωρέσουν τα μυστικά ενός και μόνο κόκκου σκόνης; Μπορούν να προσεγγίσουν την πολυπλοκότητα που κρύβεται και μόνο εκεί;

Άρα, τελικά, ο άνθρωπος είναι ανθρωπάκος;

Μάλλον όχι. Γιατί, αν εκεί έξω υπάρχουν δισεκατομμύρια δισεκατομμυρίων ήλιοι, οι νευρωνικές συνάψεις του ανθρώπινου εγκεφάλου «εδώ μέσα» προσεγγίζουν το ένα πεντάκις εκατομμύριο. Ο άνθρωπος έχει τη δυνατότητα να εξελιχθεί είτε σε ανθρωπάκο είτε σε Άνθρωπο.

Στην πρώτη περίπτωση, παροπλίζοντας το μεγαλύτερο μέρος αυτού του πεντάκις εκατομμυρίου των συνάψεων, επιφυλάσσει στον εαυτό του την τύχη του περιφερόμενου πεπτικού σωλήνα. Εδώ κρύβεται και το βαθύτερο νόημα της λέξης «αμαρτία». Αμαρτία είναι το να καταδικάσεις ένα αετόπουλο να ζει σε ένα κοτέτσι, ψαλιδίζοντας του τα φτερά και πείθοντας το ότι είναι κότα. Αμαρτία είναι να μάθεις το αετόπουλο να κάνει παρέα με κότες, να δέχεται εντολές από κότες, να κακαρίζει όπως αυτές, να περνάει τις μέρες του αναζητώντας σκουλήκια, και τις νύχτες κουρνιασμένο στο κοτέτσι. Αμαρτία είναι να καταδικάσεις το αετόπουλο να συμμορφώνεται με τις υποδείξεις του εκάστοτε κόκορα, χωρίς ποτέ να μάθει τι θα σήμαινε να πετάει.

Στη δεύτερη περίπτωση; Α, ποιος ξέρει; Οι άνθρωποι που βαδίζουν στα σχετικά μονοπάτια δεν αρκούνται σε θεωρητικολογίες. Ενδεικτικό είναι το παρακάτω δημοσίευμα της εφημερίδας "το Βήμα", φύλλο 25/10/1998.

Τα όρια ανάμεσα στη φαντασία και την πραγματικότητα έγιναν ασαφή για μια ακόμη φορά, καθώς Αμερικανοί φυσικοί πραγματοποίησαν το πρώτο πείραμα τηλεμεταφοράς. Και αν αυτό που τηλεμεταφέρθηκε δεν ήταν παρά μια δέσμη φωτός, πολλοί εκτιμούν πως ισοδυναμεί με το πρώτο βήμα (από τα πολλά, είναι η αλήθεια) για την τηλεμεταφορά ζωντανής ύλης.

Η ερευνητική ομάδα του καθηγητή της Φυσικής Τζεφ Κιμπλ, από το Τεχνολογικό Ινστιτούτο της Καλιφόρνιας (Caltech), πέτυχε για πρώτη φορά την τηλεμεταφορά φωτονίων. Με άλλα λόγια, δεν μετέφερε τα ίδια τα φωτόνια, αλλά μεταφέροντας τις ιδιότητές τους δημιούργησε όμοιά τους σε απόσταση ενός μέτρου. Το πείραμα περιγράφεται στο τελευταίο τεύχος της επιστημονικής επιθεώρησης «Science» ως η επιτυχημένη μεταφορά μιας κβαντικής κατάστασης φωτός από το ένα άκρο ενός οπτικού πάγκου στο άλλο, χωρίς αυτή να διασχίσει ένα φυσικό μέσο στο ενδιάμεσο.

Στην προκειμένη περίπτωση, η απόσταση ήταν μόνον ένα μέτρο, αλλά, σύμφωνα με τους Αμερικανούς ερευνητές, «το ίδιο σχήμα θα μπορούσε να δουλέψει και σε πολύ μεγαλύτερες αποστάσεις. Η δουλειά αυτή αποτελεί ένα σημαντικό βήμα για την πραγματοποίηση δικτύων τα οποία θα μεταδίδουν κβαντική πληροφορία, ένα είδος κβαντικού διαδικτύου».

Το πείραμα των φυσικών του Caltech βασίστηκε σε μια περίεργη ιδιότητα των ατομικών σωματιδίων, η οποία ονομάζεται quantum entanglement και η οποία περιγράφει τη σχέση δύο σωματιδίων τα οποία συμπεριφέρονται ως κβαντικοί δίδυμοι : αν και βρίσκονται μακριά το ένα από το άλλο, σχετίζονται κατά τρόπον ώστε οι ιδιότητες του ενός να επηρεάζουν το άλλο. Όπως χαρακτηριστικά δήλωσε ο καθηγητής Κιμπλ εξηγώντας το φαινόμενο, «entanglement θα πει πως αν γαργαλήσεις τον έναν, γελάει ο άλλος». Στην πράξη το πείραμα δεν είναι τίποτε άλλο παρά η πρώτη πειραματική απόδειξη της ιδιότητας του entanglement, που ως τώρα ήταν μόνο θεωρητική πιθανότητα.

Αυτό που έκαναν οι Αμερικανοί φυσικοί ήταν να δημιουργήσουν δύο δέσμες φωτός, οι οποίες λειτουργούν κβαντικά ως πομπός και δέκτης και στις οποίες έδωσαν ανθρώπινα ονόματα. Ο πομπός ονομάστηκε Alice και ο δέκτης Bob. Αν η Alice ήταν όντως το κβαντικό δίδυμο του Bob, θα έπρεπε μια κβαντική κατάσταση η οποία θα επηρέαζε την Alice να είχε το ίδιο ακριβώς αποτέλεσμα και στον Bob. Το πρόβλημα όμως με τα κβαντικά δίδυμα είναι πως η ίδια η διαδικασία της μέτρησης καθίσταται αδύνατη, αφού προκαλεί αλλαγές στο σύστημα. Το τέχνασμα το οποίο χρησιμοποιήθηκε προκειμένου να γίνουν μετρήσεις ήταν η χρησιμοποίηση ενός τρίτου κβαντικού «προσώπου», του Victor. O Victor δημιουργεί και στέλνει μια άγνωστη πληροφορία στην Alice και στη συνέχεια ελέγχει την πληροφορία η οποία εξέρχεται από τον Bob. Αν η Alice και ο Bob αποτελούν κβαντικούς διδύμους, η πληροφορία (η οποία θα έχει τηλεμεταφερθεί) θα είναι ακριβώς η ίδια και ο Victor είναι ο μόνος που μπορεί να το ελέγξει, δεδομένου ότι εκείνος τη δημιούργησε και την έστειλε στον Bob μέσω της Alice.

Εκτός από την αξία του αυτή καθεαυτή, το πείραμα των ερευνητών του Ca1tech μπορεί να αποτελέσει τη βάση για τη δημιουργία κβαντικών ηλεκτρονικών υπολογιστών, οι οποίοι δεν θα χρειάζονται μικροτσίπ και καλώδια για τη μεταφορά της πληροφορίας και των οποίων οι ταχύτητες θα ξεπερνούν κατά πολύ αυτές των σημερινών. Η ιδέα αυτών των υπολογιστών ξεκίνησε μόλις το 1993 και η επιτυχία του πειράματος αποτελεί στην ουσία την πρώτη απόδειξη πως θα μπορούσε και να είναι υλοποιήσιμη. Όπως χαρακτηριστικά δήλωσε ένας από τους συνεργάτες του καθηγητή Κιμπλ : «Το να καταστήσουμε την κβαντική τηλεμεταφορά από μια αμιγώς θεωρητική ιδέα σε μια πειραματική πραγματικότητα, έφερε τον κβαντικό κόσμο λιγάκι πιο κοντά στην καθημερινή μας ζωή». Δυστυχώς, όχι τόσο κοντά ώστε να τηλεμεταφερόμαστε και εμείς από το γραφείο στο σπίτι εν ριπή οφθαλμού...

Μερικά από τα πλέον απόρρητα και ακριβοπληρωμένα προγράμματα παγκοσμίως αφορούν πιθανές εφαρμογές όσων προβλέπει η Κβαντική Φυσική. Και δεν είναι, βέβαια, μόνο η επιστήμη· προσεγγίσεις στις οποίες η επιστημονική ανάλυση φτάνει μόλις στις μέρες μας απαντώνται σε ολόκληρο το φάσμα της ανθρώπινης νόησης. Ζητήματα φιλοσοφικά/θεολογικά, όπως η απροσδιοριστία ή η ελεύθερη βούληση, θέματα που άπτονται της σύνδεσης του νου με την ύλη, κοσμολογικές αντιλήψεις του τύπου της Γενικής Σχετικότητας και της Χαολογίας – όλα αυτά δεν είναι ακριβώς καινούρια· οι ίδιες γενικές αρχές, οι ίδιες ευρύτερες αναζητήσεις, υπάρχουν εγγεγραμμένες σε παραδόσεις και διδασκαλίες όλων των αρχαίων πολιτισμών. Αναμεμιγμένες συνήθως με μυθολογικά στοιχεία, δοσμένες μέσα από διαφορετικά ονόματα και ορολογίες, η κεντρική ιδέα είναι πάντα ίδια: μιλούν για μια άπιαστη κοσμική Πραγματικότητα, για μια βαθύτερη κατανόηση που χάθηκε, και για την προσπάθεια του ανθρώπου να την ξανακερδίσει.

09/11/2003